Blog 3

Hello everybody, its been awhile since I last blogged. So, for this week's blog, I will be covering a new topic, Design of Experiment (DOE). Using FULL FACTORIAL and FRACTIONAL FACTORIAL data analysis, I will be solving the case study provided below, enjoy the learning journey!

CASE STUDY

What could be simpler than making microwave popcorn? Unfortunately, as everyone who has ever made popcorn knows, it’s nearly impossible to get every kernel of corn to pop. Often a considerable number of inedible “bullets” (un-popped kernels) remain at the bottom of the bag. What causes this loss of popcorn yield? In this case study, three factors were identified:

FACTORS	LOW (-)	HIGH (+)
A - Diameter of bowls to contain the corn	10cm	15cm
B - Microwaving time	4minutes	6minutes
C - Power setting of microwave	75%	100%

8 runs were performed with 100 grams of corn used in every experiments and the measured variable is the amount of “bullets” formed in grams and data collected are shown below:

Run order	A	B	C	Bullets (grams)
1	+	-	-	3.50
2	-	+	-	2.50
3	-	-	+	0.74
4	+	+	-	1.50
5	+	-	+	0.95
6	+	+	+	0.32
7	-	+	+	0.50
8	-	-	-	3.12

FULL FACTORIAL

What is full factorial???... In a full factorial design, every possible combination of the levels of each factor is investigated. Although it gives the best and most reliable results, full factorial can be time consuming depending on the number of possible combination experiments. The number of experiment (N) can be calculated by using this formula:

Link to excel file : DOE For Full Factorial .xlsx

Here are the high and low average mass for individual factors:

From the graph above, we can infer that 

• When the diameter increases from 10cm to 15cm, the mass of "bullets" decreases from 1.72g to 1.5675g.

• When the microwaving time increases from 4minutes to 6minutes, the mass of "bullets" decreases from 2.08g to 1.205g.

• When the power setting of the microwave increases from 75% to 100% , the mass of "bullets" decreases from 2.66g to 0.6275g.

Significant Ranking:

Most significant is microwave power, second most significant is microwaving time and least significant is diameters of bowl to contain the corn

Right now i will be talking about Interaction Effects, so you might wonder.. what is interaction effects?..

Simply put, interaction effects occur when the impact of changing one factor depends on the level of another factor. It means factors don't act independently but affect outcomes differently when combined.

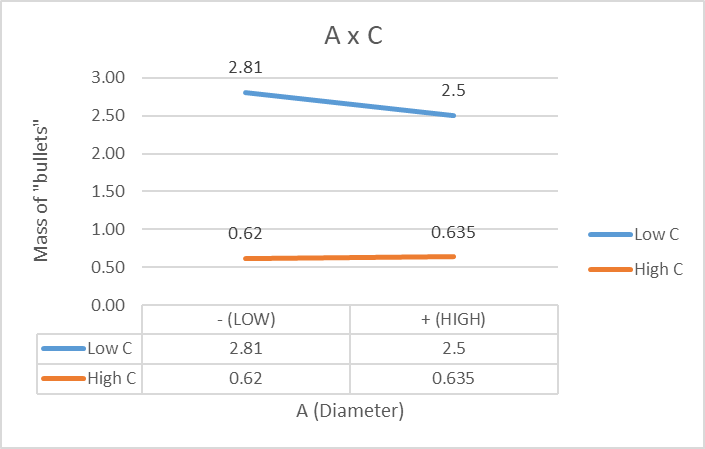
So below are the different interaction between different factors.

Interaction effects:

In conclusion, for Full Factorial data analysis, the power setting of the microwave plays the most significant role in decreasing the mass of "bullets" followed by microwaving time and lastly, diameter. From my data, the best way to make popcorns is where the 3 factors are at high Diameter of 15cm (+), 6 Minutes of microwaving time (+) and lastly 100% Power setting of the microwave (+). This is complimented from the graphs for interaction effects as it shows that both factors at high(+) will give the most significance..

That is all for Full Factorial, now lets jump right into Fractional Factorial

Fractional Factorial

What is fractional factorial???...A fractional factorial is ‘less than full’. Fewer than all possible treatments are chosen to still provide sufficient information to determine the factor effect. It is more efficient and resource-effective, but you risk missing information.

Note: I will be using runs 2,3,5 and 8 for fractional factorial design

Excel File: DOE For Fractional Factorial .xlsx

Here are the high and low average mass for individual factors:

From the graph above, we can infer that 

• When the diameter increases from 10cm to 15cm, the mass of "bullets" decreases from 0.81g to 0.955g.

• When the microwaving time increases from 4minutes to 6minutes, the mass of "bullets" decreases from 1.06g to 0.705g.

• When the power setting of the microwave increases from 75% to 100% , the mass of "bullets" decreases from 1.5g to 0.265g.

Significant Ranking:

Most significant is microwave power, second most significant is microwaving time and least significant is diameters of bowl to contain the corn

In conclusion, the data for fractional factorial analysis is slightly different as when the diameter of the bowl increases, the mass of bullets increases from 0.81g to 0.955g which theoretically does not make sense as higher diameter gives a higher surface area so that more corn can become popcorn so the mass of the "bullets" should decrease instead. However the most significant and second most significant factor still does not change in ranking. So if i were to use fractional factorial design, the best run would be run 7.

Learning reflection:

Reflecting on the Design of Experiments (DOE) practical and lecture, I'm grateful for acquiring this new skillset. While I may not be proficient in Excel, I now have a basic understanding of both full and fractional factorial designs. In real-world scenarios, conducting a full factorial experiment isn't feasible due to time and resource constraints. This is where fractional factorial designs, with their orthogonal balance, comes into play. While they may not be as reliable as full factorial designs, they still yield results akin to them.

During our practical session, my partner Jing Yue and I were tasked with implementing a full factorial design. Through our experiments and subsequent analysis, we discovered that arm length had the most significant impact, followed by stop angle and projectile weight. Interestingly, contrary to our initial beliefs, longer arm lengths projected the projectile a shorter distance, emphasizing the importance of testing factors over assumptions.

My favorite part of the practical was the group challenge, where each group had to hit targets using data from our experiments. Utilizing our experiment data, my group successfully hit all targets, showcasing the practical application of DOE.

In conclusion, DOE is crucial for optimizing resources, identifying key factors, and solving complex problems across industries. I look forward to applying this skill in my future endeavors, including my Final Year Project and beyond.

Thankyou for sticking with me to the end of this blog, I hope you learnt something new today and appreciate the importance of DOE. Stay tune for the next blog about hypothesis testing.